Hệ thức Viet và ứng dụng: Lý thuyết, Bài tập và Cách giải hệ thức Viet

Hệ thức Viet và ứng dụng là một trong những chuyên đề cơ bản nhưng quan trọng trong chương trình toán 9 và thi tuyển sinh vào lớp 10. Vậy cụ thể hệ thức Viet là gì? Những ứng dụng của hệ thức Viet ? Cách giải hệ thức Viet như nào?… Trong nội dung bài viết dưới đây, DINHNGHIA.VN sẽ giúp bạn tổng hợp kiến thức về chủ đề trên, cùng tìm hiểu nhé!

Hệ thức Viet là gì?

Hệ thức Viet do nhà Toán học François Viète tìm ra, nói lên mối quan hệ giữa các nghiệm với các hệ số của đa thức. Trong chương mình phổ thông thì hệ thức Viet đối với phương trình bậc hai thường được sử dụng hơn cả. Hệ thức Viet được phát biểu như sau:

Cho phương trình bậc \( 2: \) \( ax^2+bx+c \) có hai nghiệm \( x_1;x_2 \). Khi đó :

\(\left\{\begin{matrix} x_1+x_2=-\frac{b}{a}\\ x_1.x_2=\frac{c}{a} \end{matrix}\right.\)

Cách giải hệ thức Viet

Trong các bài toán ứng dụng hệ thức Viet, chúng ta cần biến đổi các đại lượng yêu cầu của bài toán về dạng \(\left\{\begin{matrix} S=x_1+x_2\\ P=x_1.x_2 \end{matrix}\right.\) để có thể áp dụng được hệ thức Viet. Sau đây là một số biến đổi cơ bản:

• \( x_1^2+x_2^2=S^2-2P \)

• \((x_1-x_2)^2= S^2-4P\)

• \(x_1^2-x_2^2=S.\sqrt{S^2-4P}\)

• \(x_1^3+x_2^3=S(S^2-3P)\)

• \(\frac{1}{x_1}+\frac{1}{x_2}= \frac{S}{P}\)

Ứng dụng hệ thức Viet

Nhẩm nghiệm của phương trình

Lập phương trình bậc hai

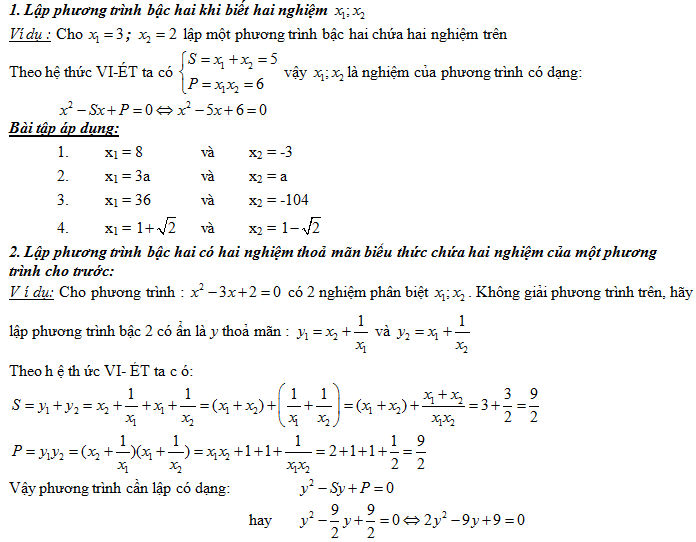
Tìm hệ thức liên hệ giữa hai nghiệm của phương trình

Tìm hai số biết tổng và tích của chúng

Bài toán: Tìm hai số biết rằng tổng của chúng bằng \( S \) và tích của chúng bằng \( P \)

Theo định lý Viet thì hai số cần tìm là nghiệm của phương trình bậc \( 2 \) :

\( x^2-Sx+P \)

***Chú ý: Điều kiện để tồn tại hai số đó là \( S^2-4P \geq 0 \)

Ví dụ:

Tìm hai số biết rằng chúng có tổng bằng \( 27 \) và có tích bằng \( 180 \)

Cách giải:

Theo định lý Viet thì hai số cần tìm là hai nghiệm của phương trình

\( x^2-27x+180 =0 \)

\(\Leftrightarrow (x-15)(x-12)=0\)

\(\Leftrightarrow \left[\begin{array}{l}x=15\\x=12\end{array}\right.\)

Vậy hai số cần tìm là \( 15;12 \)

Tính giá trị của các biểu thức nghiệm

Chúng ta sử dụng các biến đổi nêu trên để quy biểu thức về dạng \( S,P \) rồi từ đó tính giá trị của biểu thức 

Ví dụ 3:

Cho phương trình \( x^2-(m+2)x+(m+3)^2 \) có hai nghiệm phân biệt \( x_1;x_2 \)

Chứng minh rằng với mọi giá trị của \( m \) thỏa mãn phương trình đã cho có nghiệm thì giá trị của biểu thức

\(A=\frac{x_1}{x_2+1}+\frac{x_2}{x_1+1}\) luôn không đổi 

Cách giải:

Áp dụng hệ thức Viet ta có :

\(\left\{\begin{matrix} S=x_1+x_2=m+2\\ P=x_1.x_2=(m+3)^2 \end{matrix}\right.\)

Mặt khác

\(A=\frac{x_1^2+x_2^2+x_1+x_2}{x_1.x_2+x_1+x_2+1}=\frac{S^2+S-2P}{S+P+1}\)

Thay vào ta được

\(A=\frac{(m+2)^2+m+2-2(m+3)^2}{(m+3)^2+m+2+1}\)

\(=-\frac{m^2+7m+12}{m^2+7m+12}=-1\)

Vậy \(A=-1\)

Tìm giá trị tham số thỏa mãn biểu thức chứa nghiệm

Bài toán: Cho phương trình bậc hai : \( ax^2+bx+c \) với \( a,b,c \) là các hệ số chưa tham số \( m \) . Tìm \( m \) để phương trình đã cho có hai nghiệm \( x_1;x_2 \) thỏa mãn hệ thức \( K \)

Các bước giải:

• Bước 1: Tìm điều kiện của \( m \) để phương trình có hai nghiệm

• Bước 2: Biến đổi \( K \) về dạng \( S, P \) với \(\left\{\begin{matrix} S=x_1+x_2\\P=x_1.x_2 \end{matrix}\right.\)

• Bước 3: Áp dụng hệ thức Viet để biến đổi \( K \) về phương trình ẩn \( m \) rồi giải ra tìm \( m \)

Ví dụ:

Cho phương trình : \( x^2 – (2m+1)x+m^2+2 =0 \) . Tìm \( m \) để phương trình đã cho có hai nghiệm phân biệt \( x_1;x_2 \) thỏa mãn

\(3x_1x_2-5(x_1+x_2)+7=0\)

Cách giải:

Để phương trình đã cho có hai nghiệm phân biệt thì

\(\Delta = (2m+1)^2-4(m^2+2)>0\)

\(\Leftrightarrow 4m-7 >0 \Leftrightarrow m >\frac{7}{4} \hspace{1cm} (1)\)

Áp dụng đinh lý Viet ta có

\(\left\{\begin{matrix} x_1+x_2 =2m+1\\x_1.x_2=m^2+2 \end{matrix}\right.\)

Thay vào ta được :

\(3x_1x_2-5(x_1+x_2)+7=0 \Leftrightarrow 3(m^2+2)-5(2m+1)+7=0\)

\(\Leftrightarrow 3m^2-10m+8=0\)

\(\Leftrightarrow (3m-4)(m-2)=0 \Leftrightarrow \left[\begin{array}{l}m=2\\m=\frac{4}{3}\end{array}\right.\)

Kết hợp với \( (1) \) ta được \( m=2 \)

Xác định dấu các nghiệm của phương trình bậc hai

Cho phương trình bậc hai \( ax^2+bx+c \) có hai nghiệm phân biệt \( x_1;x_2 \). Theo định lý Viet có :

\(\left\{\begin{matrix} S=x_1+x_2=-\frac{b}{a}\\ P=x_1x_2=\frac{c}{a} \end{matrix}\right.\)

Khi đó:

• \( x_1; x_2 \) cùng dương \(\Leftrightarrow \left\{\begin{matrix} S=-\frac{b}{a}>0\\ P=\frac{c}{a}>0 \end{matrix}\right.\)

• \( x_1; x_2 \) cùng âm \(\Leftrightarrow \left\{\begin{matrix} S=-\frac{b}{a}<0\\ P=\frac{c}{a}>0 \end{matrix}\right.\)

• \( x_1; x_2 \) trái dấu \(\Leftrightarrow P=x_1.x_2<0\)

Ví dụ:

Tìm \( m \) để phương trình \( (m-1)x^2+2x+m =0 \) có ít nhất một nghiệm không âm

Cách giải:

Xét \( m=1 \) phương trình đã cho trở thành

\(2x+1=0\Leftrightarrow x=-\frac{1}{2}\) ( loại )

Xét \(m \neq 1\). Để phương trình có nghiệm thì

\(\Delta’ =1-m(m-1) \geq 0\)

\(\Leftrightarrow m^2-m-1 \leq 0\)

\(\Leftrightarrow m \in [\frac{1-\sqrt{5}}{2};\frac{1+\sqrt{5}}{2}] \hspace{1cm} (1) \)

Theo định lý Viet thì:

\(\left\{\begin{matrix} x_1+x_2 =-\frac{2}{m-1}\\ x_1x_2=\frac{m}{m-1} \end{matrix}\right.\)

Để phương trình có ít nhất một nghiệm không âm thì

\(\left[\begin{array}{l}x_1x_2 \leq 0 \\ \left\{\begin{matrix} x_1x_2>0\\ x_1+x_2 \leq 0 \end{matrix}\right.\end{array}\right.\)

\(\Leftrightarrow \left[\begin{array}{l} -\frac{2}{m-1} \leq 0 \\ \left\{\begin{matrix} -\frac{2}{m-1}>0\\ \frac{m}{m-1} \leq 0 \end{matrix}\right.\end{array}\right.\)

\(\Leftrightarrow \left[\begin{array}{l} m-1 > 0 \\ \left\{\begin{matrix} m-1 <0 \\ m \in [0;1) \end{matrix}\right.\end{array}\right.\)

\(\Leftrightarrow \left[\begin{array}{l} m \geq 1 \\ m \in [0;1) \end{array}\right.\)

\(\Leftrightarrow m\geq 0 | m\neq 1\)

Kết hợp với \( (1) \) thì ta có \(m \in [0;\frac{1+\sqrt{5}}{2}]\)

Tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức chứa nghiệm

Hệ thức Viet và ứng dụng nâng cao

Tìm cực trị của biểu thức chứa nghiệm

Cách làm: Ta quy biểu thức chứa nghiệm về biểu thức theo tham số bằng cách sử dụng định lý Viet rồi từ đó tìm \(\min , \max\) của biểu thức chứa tham số đó

Ví dụ:

Cho phương trình \( x^2+(m+1)x+m =0 \). Tìm \( m \) để phương trình đã cho có hai nghiệm \( x_1;x_2 \) sao cho biểu thức \( A= x_1^2+x_2^2 \) đạt giá trị nhỏ nhất

Cách giải:

Để phương trình đã cho có hai nghiệm thì

\(\Delta = (m+1)^2-4m \geq 0\)

\(\Leftrightarrow (m-1)^2 \geq 0\). Điều này luôn đúng với mọi \(m \in \mathbb{R}\)

Áp dụng định lý Viet ta có

\(\left\{\begin{matrix} x_1+x_2=-(m+1)\\ x_1x_2= m \end{matrix}\right.\)

Thay vào ta có :

\(A=x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2\)

\(=(m+1)^2-2m =m^2+1\geq 1\)

Vậy \(A_{\min}=1 \Leftrightarrow m=0\)

Bước nhảy Viet – Vieta Jumping

Đây là phương pháp để giải các bài toán số học trong các kỳ thi HSG Quốc gia, quốc tế. Ý tưởng của phương pháp là với các phương trình nghiệm nguyên bậc hai \( 2 \) ẩn \( a,b \) thì ta coi [/latex] a [/latex] là một nghiệm theo phương trình ẩn [/latex] b [/latex]. Áp dụng đinh lý Viet thì phương trình còn một nghiệm \( a_1 \) khác. Như vậy phương trình lại có một cặp nghiệm \( (a_1;b) \). Cứ lặp lại các bước như trên thì ta sẽ lại tạo ra một cặp nghiệm mới \( (a_1;b_1) ; (a_2;b_2 ) \) . Vì từ \((a;b)\rightarrow (a_1;b_1)\) như vậy nên ta gọi phương pháp này là “ bước nhảy Viet “

Ví dụ:

Chứng minh rằng nếu \( a, b \) là các số nguyên dương sao cho \( k=\frac{a^2+b^2}{ab-1} \) là một số nguyên thì \( k=5 \)

Cách giải:

Trong tất cả các cặp số \( (a, b) \) thỏa mãn \( k \) là một số nguyên, ta chọn ra cặp \( (a, b) \) sao cho \( a+b \) là nhỏ nhất.

Xét phương trình: \( k=\frac{x^2+b^2}{xb-1}\Leftrightarrow x^2-kbx+b^2+k=0\;\;\;\;\;\;(*) \)

Rõ ràng, phương trình \( (*) \) nhận một nghiệm là \( a, \) gọi nghiệm còn lại là \( x_0 \). Theo định lý Viet, ta có:

\( \begin{cases}x_0+a=bk\\x_0.a=b^2+k\end{cases} \)

Rõ ràng, \( x_0\in\mathbb{Z^+} \)

• Nếu trong hai số \( a;b \) có một số bằng \( 1 \) giả sử \( b=1 \), thế thì: \( k=\frac{a^2+1}{a-1}=a+1+\frac{2}{a-1}\in\mathbb{Z} \)

\(\Rightarrow (a-1)\;|\;2 \Rightarrow \left[\begin{array}{l}a-1=1\\a-1=2\end{array}\right.\)

\(\Leftrightarrow \left[\begin{array}{l}a=2\\a=3\end{array}\right.\)

\( \Rightarrow k=5 \)

• Nếu \(\min (a, b)>1\), thì do: \(b^2-kb^2+b^2+k>0 \Leftrightarrow k(1-b^2)+2b^2>0\)

 Vì \(b>1 \Rightarrow b^2-1>0\Rightarrow b \geq 2\), lúc này ta có:

\(k<\frac{2b^2}{b^2-1}=\frac{2}{1-\frac{1}{b^2}}\le\frac{2}{1-\frac{1}{4}}=\frac{8}{3}\;\;\;\;\;\;\;\;\;\;(1)\)

Mặt khác, ta lại có:

\(\frac{1}{k}=\frac{ab-1}{a^2+b^2}\le \frac{ab-1}{2ab}=\frac{1}{2}-\frac{1}{ab}=\frac{1}{2}\Leftrightarrow k>2\;\;\;\;\;\;\;\;\;\;(2)\)

Từ \( (1) (2) \) suy ra điều mâu thuẫn.

Vậy ta có \( k=5 \) là giá trị duy nhất thỏa mãn bài toán

Bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp lý thuyết và bài tập về chuyên đề hệ thức Viet và ứng dụng cũng như các phương pháp giải. Hy vọng những kiến thức trong bài viết sẽ giúp ích cho bạn trong quá trình học tập và nghiên cứu về chuyên đề hệ thức Viet và ứng dụng. Chúc bạn luôn học tốt!

Rate this post

Please follow and like us: