Lực kéo về

Lực kéo về hay có tên gọi khác là lực hồi phục. Lực này xuất hiên khi vật bắt đầu rời khỏi vị trí cân bằng, nó có xu hướng đưa vật về vị trí cân bằng.

• Lực kéo về là nguyên nhân làm cho vật dao động điều hòa.
• Dấu “-” chỉ lực hướng về vị trí cân bằng.

Lưu ý:

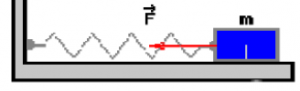
• Với con lắc lò xo có biểu thức  F = – kx.
• Với con lắc đơn thì lực kéo về có biểu thức F = – mg.sinα, trong đó α là li độ góc.
• Với con lắc lò xo nằm ngang thì lực kéo về chính là lực đàn hồi.

Chúng ta cùng nhau vào phần ví dụ để hhieeur bản chất của lực kéo về. Tất cả những ví dụ này được trích trong đề thi chính thức của BGD&ĐT.

Câu 1 [ĐỀ THI BGD&ĐT]: Một vật nhỏ có khối lượng 500 g dao động điều hòa dưới tác dụng của một lực kéo về có biểu thức F = – 0,8cos 4t (N). Dao động của vật có biên độ là
A. 6 cm
B. 12 cm
C. 8 cm
D. 10 cm
Giải
Theo đề suy ra: $\left\{ \begin{array}{l}
{F_{m{\rm{ax}}}} = kA = m{\omega ^2}.A = 0,8N\\
\omega = 4\left( {\frac{{rad}}{s}} \right)\\
m = 0,5kg
\end{array} \right. \to A = 0,1m = 10cm$

Câu 2 [ĐỀ THI BGD&ĐT]: Ở một nơi trên Trái Đất, hai con ỉắc đơn có cùng chiều dài đang đao động điều hòa với cùng biên độ. Gọi m1, F$_1$ và m2, F$_2$ lần lượt là khối lượng, độ lớn lực kéo về cực đại của con lắc thứ nhất và của con lắc thứ hai. Biết m1 + m2 = 1,2 kg và 2F$_2$ = 3F$_1$ . Giá trị của m1 là
A. 720 g.
B. 400g.
C. 480 g.
D. 600 g.
Giải
Ở một nơi trên Trái Đất, hai con ỉắc đơn có cùng chiều dài →cùng tần số góc
$\left\{ \begin{array}{l}
{F_{1\max }} = {m_1}{\omega ^2}A\\
{F_{2\max }} = {m_2}{\omega ^2}A
\end{array} \right. \to \frac{{{F_{1\max }}}}{{{F_{2\max }}}} = \frac{{{m_1}}}{{{m_2}}} = \frac{2}{3} \to \frac{{{m_1}}}{{1,2 – {m_1}}} = \frac{2}{3} \to {m_1} = 0,48kg = 480g$
Chọn C.

Câu 3 [ĐỀ THI BGD&ĐT]: Một chất điểm dao động điều hòa trên trục Ox nằm ngang với động năng cực đại W0, lực kéo về có độ lớn cực đại F0. Vào thời điểm lực kéo về có độ lớn bằng một nửa F0 thì động năng của vật bằng
A. $\frac{{2{W_0}}}{3}$
B. $\frac{{3{W_0}}}{4}$
C. $\frac{{{W_0}}}{3}$
D. $\frac{{{W_0}}}{2}$
Giải
Do chất điểm dao động điều hòa theo phương ngang nên lực kéo về có độ lớn: |F| = mω2.|x|
$\begin{array}{l}
F = \frac{{{F_0}}}{2} \leftrightarrow m{\omega ^2}\left| x \right| = \frac{1}{2}m{\omega ^2}A \leftrightarrow \left| x \right| = \frac{A}{2} \to \left| v \right| = \frac{{\sqrt 3 \omega A}}{2}\\
\to {{\rm{W}}_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{\left( {\frac{{\sqrt 3 \omega A}}{2}} \right)^2} = \frac{3}{4}\frac{1}{2}m{\omega ^2}{A^2} = \frac{3}{4}{{\rm{W}}_0}
\end{array}$

Câu 4 [ĐỀ THI BGD&ĐT]: Ở một nới trên Trái Đất, hai con lắc đơn có cùng khối lượng đang dao động điều hòa. Gọi ℓ$_1$, s$_{01}$, F$_1$ và ℓ$_2$, s$_{02}$, F$_2$ lần lượt là chiều dài, biên độ, độ lớn lực kéo về cực đại của con lắc thứ nhất và của con lắc thứ hai. Biết 3ℓ$_2$ = 2ℓ$_1$, 2s$_{02}$ = 3s$_{01}$. Tỉ số $\frac{{{F_1}}}{{{F_2}}}$ bằng
A. 3/2
B. 4/9
C. 9/4
D. 2/3
Giải
Vì con lắc dao động điều hòa nên
$\alpha \le {10^0} \to \sin \alpha \approx \alpha = \frac{s}{\ell } \to {F_{\max }} = mg.\frac{{{s_0}}}{\ell } \to \frac{{{F_1}}}{{{F_2}}} = \frac{{{s_{01}}}}{{{s_{02}}}}.\frac{{{\ell _2}}}{{{\ell _1}}} = \frac{4}{9}$
Chọn B.

Câu 5 [ĐỀ THI BGD&ĐT]: Cho hai vật dao động điều hòa dọc theo hai đường thẳng cùng song song với trục Ox. Vị trí cân bằng của mỗi vật nằm trên đường thẳng vuông góc với trục Ox tại O. Trong hệ trục vuông góc xOv, đường (1) là đồ thị biểu diễn mối quan hệ giữa vận tốc và li độ của vật 1, đường (2) la đồ thị biểu diễn mối quan hệ giữa vận tốc và li độ của vật 2 (hình vẽ). Biết các lực kéo về cực đại tác dụng lên hai vật trong quá trình dao động là bằng nhau. Tỉ số giữa khối lượng của vật 2 với khối lượng của vật 1 là
A.1/27.
B. 3.
C. 27.
D. 1/3
Giải
$\left. \begin{array}{l}
\left. \begin{array}{l}
{A_2} = 3{A_1}\\
{v_{1\max }} = 3{v_{2\max }} \to {A_1}.{\omega _1} = 3{A_2}.{\omega _2}
\end{array} \right\} \to \frac{{{\omega _1}}}{{{\omega _2}}} = 3\frac{{{A_2}}}{{{A_1}}} = 9\\
{F_{1\max }} = {F_{2\max }} \to {m_1}\omega _1^2{A_1} = {m_2}\omega _2^2{A_2} \to \frac{{{m_2}}}{{{m_1}}} = \frac{{\omega _1^2{A_1}}}{{\omega _2^2{A_2}}}
\end{array} \right\} \to \frac{{{m_2}}}{{{m_1}}} = {\left( 9 \right)^2}.\frac{1}{3} = 27$