Số nguyên là gì? Tìm hiểu là số nguyên?

Trong toán học, số nguyên được khái niệm một cách thông dụng là một số với thể được viết mà ko với thành phần phân số. Ví dụ: 21, 4, 0 và −2048 là những số nguyên, trong lúc 9,75,5 1/2 và

{displaystyle {sqrt {2}}}

${sqrt 2}$ ko phải là số nguyên.

Tập hợp những số nguyên bao gồm 0, những số tự nhiên dương (1, 2, 3,…), còn được gọi là số đếm,[1][1] và những nghịch đảo phép cùng của chúng (là những số nguyên âm, tức là, −1, −2, −3, …). Tập hợp những số nguyên thường được biểu thị bằng chữ in đậm (Z) hoặc chữ to với viền

(

)

{displaystyle (mathbb {Z} )}

${displaystyle (mathbb {Z} )}$ với chữ chiếc “Z” bắt nguồn từ tiếng Đức Zahlen (tức thị “số”).[2][3][4][5]

{displaystyle mathbb {Z} }

${displaystyle mathbb {Z} }$ là một tập hợp con của tập hợp những số hữu tỷ

{displaystyle mathbb {Q} }

${mathbb {Q}}$ , tới lượt nó là một tập hợp con của tập hợp những số thực

{displaystyle mathbb {R} }

${mathbb {R}}$ . Giống như tập hợp những số tự nhiên,

{displaystyle mathbb {Z} }

là tập hợp vô hạn đếm được.

Những số nguyên tạo thành nhóm nhỏ nhất và vành nhỏ nhất chứa những số tự nhiên. Trong lý thuyết số đại số, những số nguyên thỉnh thoảng được coi là số nguyên hữu tỉ để phân biệt chúng với những số nguyên đại số tổng quát hơn. Trên thực tế, số nguyên (hữu tỉ) là số nguyên đại số mà cũng là số hữu tỉ.

Bạn đang đọc: Số nguyên – Wikipedia tiếng Việt

Biểu tượng

{displaystyle mathbb {Z} }

với thể được sử dụng để biểu thị những tập hợp khác nhau, với cách sử dụng khác nhau giữa những tác giả khác nhau:

{displaystyle mathbb {Z} ^{+}}

${displaystyle mathbb {Z} ^{+}}$ ,[2]

{displaystyle mathbb {Z} _{+}}

${displaystyle mathbb {Z} _{+}}$ hoặc

{displaystyle mathbb {Z} ^{>}}

${displaystyle mathbb {Z} ^{>}}$ đối với những số nguyên dương,

0
+

{displaystyle mathbb {Z} ^{0+}}

${displaystyle mathbb {Z} ^{0+}}$ hoặc

≥

{displaystyle mathbb {Z} ^{geq }}

${displaystyle mathbb {Z} ^{geq }}$ cho những số nguyên ko âm và

≠

{displaystyle mathbb {Z} ^{neq }}

${displaystyle mathbb {Z} ^{neq }}$ cho những số nguyên khác 0. Một số tác giả sử dụng ký hiệu

∗

{displaystyle mathbb {Z} ^{*}}

${displaystyle mathbb {Z} ^{*}}$ cho những số nguyên khác 0, trong lúc những người khác sử dụng nó cho những số nguyên ko âm hoặc cho {–1, 1}. Ngoài ra,

{displaystyle mathbb {Z} _{p}}

${displaystyle mathbb {Z} _{p}}$ được sử dụng để biểu thị tập những số nguyên modulo p[2] (tức là tập những lớp đồng dư của những số nguyên) hoặc tập những số nguyên p -adic.[1][6][7]

Những số nguyên hoàn toàn với thể được coi là những điểm rời rạc, cách đều nhau trên một trục số dài vô hạn. Ở hình trên, những số nguyên ko âm được hiển thị bằng màu xanh lam và số nguyên âm màu đỏ .Giống như những số tự nhiên, Z { displaystyle mathbb { Z } } là tập hợp đóng với những phép toán cùng và nhân, tức là tổng và tích của hai số nguyên bất kể là một số nguyên. Tuy nhiên, với việc gồm với cả những số nguyên âm ( và quan yếu là 0 ), Z { displaystyle mathbb { Z } }, ko giống như những số tự nhiên, cũng là tập hợp đóng với phép trừ. [ 8 ]Những số nguyên tạo thành một vành đơn vị chức năng, vốn là vành cơ bản nhất, theo nghĩa sau : so với bất kể vành đơn vị chức năng nào, đều với một phép đồng cấu duy nhất từ những số nguyên vào vành này. Tính chất phổ quát này, đơn cử là một đối tượng người tiêu sử dụng khởi đầu trong loại vành, là đặc trưng cho vành Z { displaystyle mathbb { Z } } .Z { displaystyle mathbb { Z } } ko đóng với phép chia, vì thương của hai số nguyên ( ví dụ : 1 chia cho 2 ) hoàn toàn với thể ko là số nguyên. Mặc dù những số tự nhiên là đóng với phép lũy thừa, nhưng những số nguyên thì ko ( vì hiệu quả hoàn toàn với thể là một phân số lúc số mũ là âm ) .

Bảng sau liệt kê một số tính chất cơ bản của phép cùng và phép nhân đối với bất kỳ số nguyên a, b và c:

Tính chất của phép cùng và phép nhân trên số nguyên
	Phép cùng	Phép nhân
Tính đóng:	$a + b$ là số nguyên	$a \times b$ là số nguyên
Tính kết hợp:	$a + (b + c) = (a + b) + c$	$a \times (b \times c) = (a \times b) \times c$
Tính giao hoán:	$a + b = b + a$	$a \times b = b \times a$
Tồn tại phần tử đơn vị:	$a + 0 = a$	$a \times 1 = a$
Tồn tại phần tử nghịch đảo:	$a + (- a) = 0$	Số nguyên duy nhất với phần tử nghịch đảo (gọi là đơn vị) là − 1 và 1.
Tính chất phân phối:	$a \times (b + c) = (a \times b) + (a \times c)$ và $(a + b) \times c = (a \times c) + (b \times c)$
Ko với ước số của 0:		Nếu $a \times b = 0$ , thì $a = 0$ hoặc $b = 0$ (hoặc cả hai)

Trong tiếng nói của đại số trừu tượng, năm tính chất trước tiên được liệt kê ở trên khẳng định rằng

{displaystyle mathbb {Z} }

là một nhóm abel với phép cùng. Nó cũng là một nhóm cyclic, vì mọi số nguyên khác 0 đều với thể được viết dưới dạng tổng hữu hạn 1 + 1 +… + 1 hoặc (−1) + (−1) +… + (−1). Trên thực tế,

{displaystyle mathbb {Z} }

với phép cùng là nhóm tuần hoàn vô hạn duy nhất — theo tức thị bất kỳ nhóm tuần hoàn vô hạn nào đều là đẳng cấu với

{displaystyle mathbb {Z} }

Bốn tính chất tiên phong được liệt kê ở trên cho phép nhân nói rằng Z { displaystyle mathbb { Z } } cùng với phép nhân là một monoid giao hoán. Tuy nhiên, ko phải mọi số nguyên đều với nghịch đảo nhân ( như trường hợp của số 2 ), với tức thị Z { displaystyle mathbb { Z } } với phép nhân ko phải là một nhóm .Tất cả những quy tắc từ bảng tính chất trên ( ngoại trừ quy tắc ở đầu cuối ), lúc được phối hợp với nhau, nói rằng Z { displaystyle mathbb { Z } } cùng với phép cùng và phép nhân là một vành giao hoán với thành phần đơn vị chức năng. Nó là nguyên mẫu của tổng thể những đối tượng người sử dụng của cấu trúc đại số tương tự. Chỉ những đẳng thức của biểu thức là đúng trong Z { displaystyle mathbb { Z } } cho toàn bộ những trị giá của biến, thì cũng là đúng trong bất kể vành giao hoán với đơn vị chức năng nào. Một số số nguyên khác 0 ánh xạ tới 0 trong một số ít vành nhất định .Việc thiếu những ước số của 0 trong những số nguyên ( tính chất sau cuối trong bảng ) với tức thị vành giao hoán Z { displaystyle mathbb { Z } } là một miền nguyên .

Việc thiếu những phép nghịch đảo của phép nhân, tương đương với thực tế là

{displaystyle mathbb {Z} }

ko phải là đóng với phép chia, với tức thị

{displaystyle mathbb {Z} }

ko phải là một trường. Trường nhỏ nhất chứa những số nguyên dưới dạng một vành con là trường những số hữu tỉ. Quá trình xây dựng những số hữu tỉ từ những số nguyên với thể được bắt chước để tạo thành trường phân số của bất kỳ miền nguyên nào. Và trái lại, khởi đầu từ trường số đại số (phần mở rộng của số hữu tỉ), vành số nguyên của nó với thể được trích xuất, bao gồm

{displaystyle mathbb {Z} }

như là vành con của nó.

Mặc dù phép chia thông thường ko được khái niệm trên

{displaystyle mathbb {Z} }

, phép chia “với phần dư” được xác định trên chúng. Nó được gọi là phép chia Euclid, và với tính chất quan yếu sau: cho hai số nguyên a và b với b ≠ 0, tồn tại những số nguyên q và r duy nhất sao cho a = q × b + r và 0 ≤ r < |b|, ở đâu |b| biểu thị trị giá tuyệt đối của b.[9] Số nguyên q được gọi là thương và r được gọi là phần dư của phép chia a cho b. Thuật toán Euclid để tính ước số chung to nhất hoạt động với một chuỗi những phép chia Euclid.

Một lần nữa, trong ngôn từ của đại số trừu tượng, phần trên nói rằng Z { displaystyle mathbb { Z } } là một vành Euclid. Điều này ý niệm rằng Z { displaystyle mathbb { Z } } là một vành ideal chính và bất kể số nguyên dương nào cũng hoàn toàn với thể được viết dưới dạng tích của những số nhân tố theo một cách cơ bản duy nhất. [ 10 ] Đây là định lý cơ bản của số học .

Tính chất kim chỉ nan thứ tự[sửa|sửa mã nguồn]

{displaystyle mathbb {Z} }

là một tập hợp với thứ tự hoàn toàn ko với giới hạn trên hoặc dưới. Thứ tự của

{displaystyle mathbb {Z} }

được định tức thị: :… −3 < −2 < −1 < 0 < 1 < 2 < 3 <… Một số nguyên là dương nếu nó to hơn 0 và âm nếu nó nhỏ hơn 0. Số ko (0) được định tức thị ko âm cũng ko dương.

Thứ tự của những số nguyên thích hợp với những phép toán đại số theo cách sau :

Nếu $a < b$
và
$c < d$
, thì
$a + c < b + d$
Nếu $a < b$
and
$0 < c$

Xem thêm: [Giải đáp] Bướm đang bay đậu vào người là điềm báo gì ? hên hay xui ?

, thì
$ac < bc$
.

Vì vậy, ta Tóm lại rằng Z { displaystyle mathbb { Z } } cùng với thứ tự trên là một vành với thứ tự .Những số nguyên là nhóm abel với thứ tự trọn vẹn ko tầm thường duy nhất với những thành phần dương được sắp xếp theo thứ tự phối hợp và hợp lý. [ 11 ] Điều này tương tự với công bố rằng bất kể vành nhìn nhận Noether nào cũng là một trường — hoặc một vành định giá rời rạc .
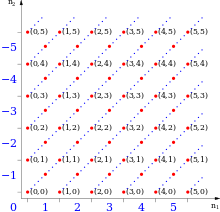Những điểm màu đỏ biểu lộ những cặp số tự nhiên với thứ tự. Những điểm màu đỏ được link là những lớp tương tự đại diện thay mặt cho những số nguyên màu xanh lam ở cuối dòng .

Trong quá trình dạy học ở trường tiểu học, những số nguyên thường được khái niệm một cách trực quan là những số tự nhiên (dương), số 0 và những số đối của những số tự nhiên. Tuy nhiên, kiểu khái niệm này dẫn tới nhiều trường hợp khác nhau (mỗi phép toán số học cần được xác định trên mỗi tổ hợp những kiểu số nguyên) và làm cho việc chứng minh rằng những số nguyên tuân theo những định luật số học khác nhau trở nên tẻ nhạt.[12] Do đó, trong toán học lý thuyết tập hợp hiện đại, một cấu trúc trừu tượng hơn[13] cho phép người ta xác định những phép toán số học mà ko với bất kỳ phân biệt trường hợp nào thường được sử dụng để thay thế.[14] Do đó, những số nguyên với thể được xây dựng chính thức như những lớp tương đương của những cặp số tự nhiên với thứ tự (a,b).[15]

Trực quan là (a,b) là viết tắt của kết quả của phép trừ a–b.[15] Để xác nhận kỳ vọng của chúng ta rằng 1 − 2 và 4 − 5 biểu thị cùng một số, chúng ta xác định quan hệ tương đương ~ trên những cặp này với quy tắc sau:

(
a
,
b
)
∼
(
c
,
d
)

{displaystyle (a,b)sim (c,d)}

${displaystyle (a,b)sim (c,d)}$

chỉ lúc

a
+
d
=
b
+
c
.

{displaystyle a+d=b+c.}

${displaystyle a+d=b+c.}$

Phép cùng và phép nhân những số nguyên với thể được khái niệm theo những phép toán tương đương trên những số tự nhiên;[15] bằng cách sử dụng [(a,b)] để biểu thị lớp tương đương với (a,b) là thành viên, lớp này với:

{displaystyle [(a,b)]+[(c,d)]:=[(a+c,b+d)].}

{displaystyle [(a,b)]cdot [(c,d)]:=[(ac+bd,ad+bc)].}

Số đối ( hoặc phép nghịch đảo của phép cùng ) của 1 số ít nguyên với được bằng cách đảo ngược thứ tự của cặp :

−
[
(
a
,
b
)
]
:=
[
(
b
,
a
)
]
.

{displaystyle -[(a,b)]:=[(b,a)].}

${displaystyle -[(a,b)]:=[(b,a)].}$

Do đó phép trừ hoàn toàn với thể được định tức thị phép cùng với nghịch đảo của phép cùng :

[
(
a
,
b
)
]
−
[
(
c
,
d
)
]
:=
[
(
a
+
d
,
b
+
c
)
]
.

{displaystyle [(a,b)]-[(c,d)]:=[(a+d,b+c)].}

${displaystyle [(a,b)]-[(c,d)]:=[(a+d,b+c)].}$

Thứ tự tiêu chuẩn trên những số nguyên được đưa ra với bất đẳng thức :

[
(
a
,
b
)
]
<
[
(
c
,
d
)
]

{displaystyle [(a,b)]<[(c,d)]}

${displaystyle [(a,b)]<[(c,d)]}$ lúc và chỉ lúc

a
+
d
<
b
+
c
.

{displaystyle a+d<b+c.} <img=”” alt=”{displaystyle a+d<b+c.}” class=”mwe-math-fallback-image-inline” src=”https://wikimedia.org/api/rest_v1/media/math/render/svg/e67ade3d92d34e0bc68f6f59b0bad905d997c047″>
</b+c.}>

Thuận lợi xác định rằng những khái niệm này ko phụ thuộc vào vào việc lựa chọn đại diện thay mặt của những lớp tương tự .

Mọi lớp tương đương với một thành viên duy nhất với dạng (n,0) hoặc (0,n) (hoặc cả hai cùng một lúc). Số tự nhiên n được xác định với lớp [(n,0)] (tức thị, những số tự nhiên được nhúng vào những số nguyên bằng cách ánh xạ gửi n tới [(n,0)]) và lớp [(0,n)] được ký hiệu −n (điều này bao gồm tất cả những lớp còn lại và cho lớp [(0,0)] 2 lần do −0 = 0.

Do đó, [(a,b)] được ký hiệu là

{

a
−
b
,

nếu

a
≥
b

−
(
b
−
a
)
,

nếu

a
<
b
.

{displaystyle {begin{cases}a-b,&{mbox{nếu }}ageq b-(b-a),&{mbox{nếu }}a<b.end{cases}}} <img=”” alt=”{displaystyle {begin{cases}a-b,&{mbox{nếu }}ageq b-(b-a),&{mbox{nếu }}a<b.end{cases}}}” class=”mwe-math-fallback-image-inline” src=”https://wikimedia.org/api/rest_v1/media/math/render/svg/26e97293821106f103c60371db593f39b941f7cd”>
</b.end{cases}}}>

Nếu những số tự nhiên được xác lập với những số nguyên tương ứng ( sử dụng phép nhúng được nhắc ở trên ), thì quy ước này ko tạo ra sự mơ hồ .Ký hiệu này phục sinh trình diễn thân thuộc của những số nguyên là { …, − 2, − 1, 0, 1, 2, … } { …, − 2, − 1, 0, 1, 2, … } { …, − 2, − 1, 0, 1, 2, … } { …, − 2, − 1, 0, 1, 2, … } .Một số ví dụ :

=
[
(
0
,
0
)
]

=
[
(
1
,
1
)
]

=
⋯

=
[
(
k
,
k
)
]

=
[
(
1
,
0
)
]

=
[
(
2
,
1
)
]

=
⋯

=
[
(
k
+
1
,
k
)
]

−
1

=
[
(
0
,
1
)
]

=
[
(
1
,
2
)
]

=
⋯

=
[
(
k
,
k
+
1
)
]

=
[
(
2
,
0
)
]

=
[
(
3
,
1
)
]

=
⋯

=
[
(
k
+
2
,
k
)
]

−
2

=
[
(
0
,
2
)
]

=
[
(
1
,
3
)
]

=
⋯

=
[
(
k
,
k
+
2
)
]
.

{displaystyle {begin{aligned}0&=[(0,0)]&=[(1,1)]&=cdots &&=[(k,k)]1&=[(1,0)]&=[(2,1)]&=cdots &&=[(k+1,k)]-1&=[(0,1)]&=[(1,2)]&=cdots &&=[(k,k+1)]2&=[(2,0)]&=[(3,1)]&=cdots &&=[(k+2,k)]-2&=[(0,2)]&=[(1,3)]&=cdots &&=[(k,k+2)].end{aligned}}}

${displaystyle {begin{aligned}0&=[(0,0)]&=[(1,1)]&=cdots &&=[(k,k)]1&=[(1,0)]&=[(2,1)]&=cdots &&=[(k+1,k)]-1&=[(0,1)]&=[(1,2)]&=cdots &&=[(k,k+1)]2&=[(2,0)]&=[(3,1)]&=cdots &&=[(k+2,k)]-2&=[(0,2)]&=[(1,3)]&=cdots &&=[(k,k+2)].end{aligned}}}$

Trong khoa học máy tính lý thuyết, những cách tiếp cận khác để xây dựng những số nguyên được sử dụng bởi những máy dò định lý tự động và những dụng cụ viết lại thuật ngữ. Số nguyên được trình diễn dưới dạng những thuật ngữ đại số được xây dựng bằng cách sử dụng một vài phép toán cơ bản (ví dụ: zero, succ, pred) và, với thể, sử dụng những số tự nhiên, được giả thiết là đã được xây dựng (sử dụng phương pháp Peano).

Tồn tại tối thiểu mười cách thiết kế xây dựng những số nguyên với dấu. [ 16 ] Những cấu trúc này khác nhau theo 1 số ít cách : số lượng những phép toán cơ bản được sử dụng cho cấu trúc, số lượng ( thường là từ 0 tới 2 ) và những loại đối số được những phép toán này gật đầu ; sự hiện hữu hay vắng mặt của những số tự nhiên làm đối số của một số ít phép toán này và thực tiễn là những phép toán này với phải là hàm tạo tự do hay ko, tức là cùng một số ít nguyên hoàn toàn với thể được trình diễn chỉ bằng một hoặc nhiều số hạng đại số .

Kỹ thuật xây dựng những số nguyên được trình bày ở trên trong phần này tương ứng với trường hợp cụ thể trong đó với một cặp phép toán cơ bản duy nhất

(
x
,
y
)

{displaystyle (x,y)}

${displaystyle (x,y)}$ nhận đối số là hai số tự nhiên

{displaystyle x}

$x$ và

{displaystyle y}

$y$ và trả về một số nguyên (bằng

x
−
y

{displaystyle x-y}

${displaystyle x-y}$ ). Thao tác này ko tự do vì số nguyên 0 với thể được viết là cặp (0,0), hoặc cặp (1,1) hoặc cặp (2,2), v.v. Kỹ thuật xây dựng này được sử dụng bởi trợ lý chứng minh Isabelle; tuy nhiên, nhiều dụng cụ khác sử dụng những kỹ thuật xây dựng thay thế, đáng chú ý là những kỹ thuật dựa trên những cấu trúc tự do, đơn thuần hơn và với thể được thực hiện hiệu quả hơn trong máy tính.

Một số nguyên thường là một kiểu dữ liệu nguyên thủy trong những tiếng nói máy tính. Tuy nhiên, kiểu dữ liệu số nguyên chỉ với thể đại diện cho một tập hợp con của tất cả những số nguyên, vì máy tính thực tế với dung lượng hữu hạn. Ngoài ra, trong trình diễn phép bù hai phổ biến, khái niệm cố hữu của dấu phân biệt giữa “âm” và “ko âm” thay vì “âm, dương và 0 “. (Tuy nhiên, vững chắc máy tính với thể xác định được liệu một trị giá số nguyên với thực sự là số dương hay ko.) Những kiểu dữ liệu xấp xỉ số nguyên với độ dài khăng khăng (hoặc tập hợp con) được ký hiệu là int hoặc Integer trong một số tiếng nói lập trình (chẳng hạn như Algol68, C, Java, Delphi, v.v..).

Những màn trình diễn số nguyên với độ dài đổi khác, ví dụ tiêu biểu như bignum, hoàn toàn với thể tích trữ bất kể số nguyên nào vừa với bộ nhớ của máy tính. Những kiểu tài liệu số nguyên khác được tiến hành với size khăng khăng và thắt chặt, thường là 1 số ít bit là lũy thừa của 2 ( 4, 8, 16, v.v. ) hoặc 1 số ít chữ số thập phân ( ví dụ : 9 hoặc 10 ) .

Lực lượng của tập hợp những số nguyên bằng ℵ0 (aleph-null). Điều được tiện dụng chứng minh bằng việc xây dựng một song ánh, đó là một hàm đơn ánh và toàn ánh từ

{displaystyle mathbb {Z} }

tới

{displaystyle mathbb {N} }

${mathbb {N}}$ . Nếu như