Số tự nhiên – Wikipedia tiếng Việt

Những số tự nhiên tiêu dùng để đếm ( một quả táo, hai quả táo, ba quả táo …. ) .

Trong toán học, những số tự nhiên được sử dụng để đếm (như trong “sở hữu sáu đồng xu trên bàn”) và thứ tự (như trong “đây là thành xã to thứ ba trong cả nước”). Thỉnh thoảng, những số tự nhiên sở hữu thể xuất hiện dưới dạng một bộ mã thuận tiện (nhãn hoặc “tên”), tức là, như những gì những nhà tiếng nói học gọi là số danh nghĩa, loại bỏ nhiều hoặc tất cả những tính chất của một số theo nghĩa toán học. Tập hợp những số tự nhiên thường được kí hiệu bằng kí hiệu

{displaystyle mathbb {N} }

${mathbb {N}}$ .[1][2][3]

Trong tiêu chuẩn của ISO 80000-2[4] và tài liệu giáo khoa chuẩn của nước ngoài[5], số tự nhiên được định tức là những số nguyên ko âm 0, 1, 2, 3,… (thỉnh thoảng được ký hiệu chung là biểu tượng

{displaystyle mathbb {N} _{0}}

${displaystyle mathbb {N} _{0}}$ , để nhấn mạnh rằng số 0 cũng được bao gồm), trong lúc những số khác khởi đầu bằng 1, tương ứng với những số nguyên dương 1, 2, 3,… (thỉnh thoảng được ký hiệu chung bằng ký hiệu

{displaystyle mathbb {N} _{1}}

${displaystyle mathbb {N} _{1}}$ ,

{displaystyle mathbb {N} ^{+}}

${displaystyle mathbb {N} ^{+}}$ , hoặc

∗

{displaystyle mathbb {N} ^{*}}

${displaystyle mathbb {N} ^{*}}$ với nhấn mạnh rằng số 0 bị loại trừ).[6][7]

Những số tự nhiên là hạ tầng mà từ đó nhiều tập hợp số khác sở hữu thể được xây dựng bằng cách mở rộng: tập hợp những số nguyên, được xây dựng bằng cách bao gồm (nếu chưa sở hữu) phần tử trung tính 0 và một phép cùng nghịch đảo ( − n ) cho mỗi số tự nhiên khác nhau n ; tập hợp những số hữu tỉ, bằng cách bao gồm một nghịch đảo phép nhân (1/n ) cho mỗi số nguyên khác n (và cả tích của những phép nghịch đảo này với những số nguyên); tập hợp những số thực bằng cách bao gồm với những số hữu tỉ những giới hạn của (tụ họp) dãy Cauchy của những số hữu tỉ; những số phức, bằng cách cùng với những số thực căn bậc hai chưa giải của trừ một (và cả tổng và tích của chúng),…. [a] [b] Những chuỗi mở rộng này làm cho những số tự nhiên được nhúng (nhận dạng) về mặt quy tắc trong những hệ thống số khác.[8]

Bạn đang đọc: Số tự nhiên – Wikipedia tiếng Việt

Những đặc thù của số tự nhiên, ví dụ tiêu biểu như tính chia hết và phân phối của những số nhân tố, được nghiên cứu và thăm dò trong triết lý số. Những yếu tố tương quan tới việc đếm và sắp xếp thứ tự, ví dụ tiêu biểu như phân vùng và liệt kê, được nghiên cứu và thăm dò trong tổng hợp .

Theo tiếng nói thông thường, đặc trưng là trong giáo dục tiểu học, số tự nhiên sở hữu thể được gọi là số đếm[9] để loại trừ trực quan những số nguyên âm và số 0, và cũng để đối chiếu tính rời rạc của phép đếm với tính liên tục của phép đo – một đặc điểm vượt trội của số thực.

Thời cổ đại[sửa|sửa mã nguồn]

Phương pháp nguyên thủy nhất để trình diễn một số ít tự nhiên là đặt một ký hiệu cho mỗi đối tượng người tiêu tiêu dùng. Sau đó, một tập hợp những đối tượng người tiêu tiêu dùng hoàn toàn sở hữu thể được rà soát xem sở hữu bằng nhau, thừa hay thiếu — bằng cách lưu lại và xóa một đối tượng người tiêu dùng khỏi tập hợp đó .Bước tiến to tiên phong trong trừu tượng hóa là việc sử dụng những chữ số để trình diễn những số lượng. Điều này được cho phép những mạng lưới hệ thống được tăng trưởng để ghi số lượng to. Người Người nào Cập cổ đại đã tăng trưởng một mạng lưới hệ thống chữ số can đảm và mạnh mẽ với những chữ tượng hình riêng ko liên quan gì tới nhau cho 1, 10 và toàn bộ những quyền hạn của 10 tới hơn 1 triệu. Một tác phẩm chạm khắc trên đá ở Karnak, sở hữu niên đại khoảng chừng năm 1500 TCN và giờ đây là Bảo tồn Louvre ở Paris, diễn đạt 276 như 2 trăm, 7 chục và 6 đơn vị chức năng ; và tựa như cho số 4,622. Người Babylon sở hữu một mạng lưới hệ thống trị giá vị trí về cơ bản dựa trên những chữ số cho 1 và 10, sử dụng cơ số sáu mươi, với hình tượng cho 60 giống với hình tượng cho 1 — trị giá đơn cử của nó được xác lập từ văn cảnh. [ 13 ]

Một tiến bộ nữa trong việc trừu tượng hóa con số nhưng diễn ra trễ hơn nhiều: phát triển ý tưởng thể hiện số ko như là một con số với trình diễn số của riêng nó. Vào khoảng 700 TCN, những người Babylon đã tiêu dùng chữ số ko trong hệ thống ký hiệu trị giá theo vị trí nhưng một điều khá lạ là mãi cho tới lúc nền văn hóa Babylon tới hồi suy vong, người Babylon cũng chỉ biết tiêu dùng chữ số ko ở giữa những con số (ví dụ: lúc viết số 3605 họ biết đặt chữ số ko vào giữa), và chữ số này vẫn chưa bao giờ được sử dụng để làm chữ số cuối cùng của một số[14] (ví dụ: người Babylon thể hiện số 3600 và 60 như nhau – người Babylon tiêu dùng hệ cơ số 60 – để phân biệt đâu là 3600 và 60 họ phải kèm thêm một chú thích bằng lời ở dưới[15]). Những nền văn minh Olmec và Maya đã tiêu dùng số ko như là một con số riêng từ khoảng thế kỷ thứ 1 TCN (nhịn nhường như được phát triển một cách độc lập), tuy nhiên việc sử dụng này đã ko được phổ biến ra ngoài vùng Trung Bộ châu Mỹ[16][17]. Khái niệm số ko mà chúng ta hiện nay vẫn tiêu dùng xuất phát từ nhà toán học Ấn Độ Brahmagupta vào năm 628. Mặc dầu số ko đã được tiêu dùng như một con số bởi tất cả những nhà tính toán thời Trung Cổ (tiêu dùng để tính ngày Phục Sinh) mà khởi đầu là Dionysius Exiguus vào năm 525, nhưng nhìn chung vẫn ko sở hữu một chữ số La Mã nào được dành riêng để viết số ko. Thay vì vậy, thời đó người ta tiêu dùng từ Latinh là nullae, sở hữu tức là”ko sở hữu gì”để chỉ số ko.[18]

Người ta thường xem những nhà triết học Hy Lạp Pythagore và Archimedes là những người tiên phong đặt yếu tố thăm dò và nghiên cứu một cách mệnh lưới hệ thống về những số lượng như thể một thực thể trừu tượng. Tuy nhiên, cùng thời kỳ đó, một số ít nơi như Ấn Độ, Trung Quốc và Trung Bộ châu Mỹ cũng sở hữu những thăm dò và nghiên cứu độc lập tương tự như. [ 19 ]

Những khái niệm tân tiến[sửa|sửa mã nguồn]

Ở châu Âu thế kỷ 19, đã sở hữu cuộc tranh luận toán học và triết học về thực chất đúng chuẩn của những số tự nhiên. Một phe phái của chủ nghĩa tự nhiên công bố rằng những số tự nhiên là hệ quả trực tiếp của tâm ý con người. Henri Poincaré là một trong những người ủng hộ nó, cũng như Leopold Kronecker, người đã tóm tắt niềm tin của mình là ” Chúa tạo ra những số nguyên, tổng thể những thứ khác là tác phẩm của con người “. [ c ]Đối lập với những nhà Tự nhiên học, những nhà toán học thiết kế thấy cần phải cải tổ tính ngặt nghèo logic trong nền tảng của toán học. [ d ] Vào những năm 1860, Hermann Grassmann yêu cầu một khái niệm đệ quy cho những số tự nhiên, do đó nói rằng chúng ko thực sự là tự nhiên – mà là hệ quả của những khái niệm. Sau đó, hai lớp khái niệm chính thức tương tự đã được thiết kế xây dựng ; về sau, chúng vẫn được chứng tỏ là tương tự trong hầu hết những ứng dụng trong thực tiễn .Những khái niệm kim chỉ nan tập hợp về số tự nhiên được Frege khởi xướng. Ban sơ, ông khái niệm một số ít tự nhiên là lớp của tổng thể những tập hợp tương ứng 1-1 với một tập hợp đơn cử. Tuy nhiên, khái niệm này hóa ra lại dẫn tới những nghịch lý, gồm sở hữu cả nghịch lý Russell. Để tránh những nghịch lý tương tự, phép hình thức hóa đã được sửa đổi để 1 số ít tự nhiên được định tức là một tập hợp đơn cử và bất kể tập hợp nào hoàn toàn sở hữu thể được đưa vào tương ứng 1-1 với tập hợp đó được cho là sở hữu số thành phần đó. [ 22 ]Loại khái niệm thứ hai được Charles Sanders Peirce đưa ra, được Richard Dedekind tinh chỉnh, và được Giuseppe Peano mày mò thêm ; chiêu thức này giờ đây được gọi là số học Peano. Nó dựa trên tiên đề về những đặc thù của số thứ tự : mỗi số tự nhiên sở hữu một tiếp nối và mọi số tự nhiên khác 0 đều sở hữu một nhiệm kỳ trước đó duy nhất. Số học Peano tương tự với 1 số ít mạng lưới hệ thống yếu của kim chỉ nan tập hợp. Một trong những mạng lưới hệ thống tương tự là ZFC với tiên đề về vô hạn được thay thế sửa chữa bằng sự phủ định của nó. Những định lý hoàn toàn sở hữu thể được chứng tỏ trong ZFC nhưng ko hề được chứng tỏ bằng cách sử dụng Tiên đề Peano gồm sở hữu định lý Goodstein. [ 23 ]Với tổng thể những khái niệm qua tập hợp này, thật thuận tiện lúc gồm sở hữu cả số 0 ( tương ứng với tập rỗng ) vào tập hợp số tự nhiên. Bao gồm cả số 0 hiện là quy ước chung giữa những nhà kim chỉ nan tập hợp [ 24 ] và những nhà logic học. [ 25 ] Những nhà toán học khác cũng gồm sở hữu cả 0, [ e ] và những ngôn từ máy tính thường xuất phát từ 0 lúc liệt kê những mục như bộ đếm vòng lặp và thành phần chuỗi hoặc mảng. [ 26 ] [ 27 ] Mặt khác, nhiều nhà toán học đã giữ truyền thống lịch sử cũ hơn để lấy 1 là số tự nhiên tiên phong. [ 28 ]

Những nhà toán học tiêu dùng ký hiệu N hay ℕ cho tập hợp tất cả những số tự nhiên[29][30][31]. Một số văn bản cũ cũng thỉnh thoảng tiêu dùng kí hiệu J cho tập hợp này.[32] Theo khái niệm, tập hợp vô hạn và đếm được, tức lực lượng của tập hợp số tự nhiên là ℵ0

Vì những tính chất khác nhau thường được liên kết với những mã thông tin 0 và 1 (ví dụ: những phần tử trung tính cho phép cùng và phép nhân, tương ứng), điều quan yếu là phải biết phiên bản số tự nhiên nào được sử dụng trong trường hợp đang xem xét. Điều này sở hữu thể được thực hiện bằng cách giảng giải bằng văn xuôi, bằng cách viết ra tập hợp một cách rõ ràng hoặc bằng cách định danh số nhận dạng chung bằng chỉ số viết lên trên hoặc chỉ số viết xuống dưới,[33][34] chẳng hạn như thế này:

{
1
,
2
,
.
.
.
}
=

∗

∖
{
0
}
.

{displaystyle {1,2,…}=mathbb {N} ^{*}=mathbb {N} ^{+}=mathbb {N} _{0}smallsetminus {0}.}

${displaystyle {1,2,...}=mathbb {N} ^{*}=mathbb {N} ^{+}=mathbb {N} _{0}smallsetminus {0}.}$

{
0
,
1
,
2
,
.
.
.
}
=

∗

∪
{
0
}

{displaystyle ;{0,1,2,…}=mathbb {N} _{0}=mathbb {N} ^{0}=mathbb {N} ^{*}cup {0}}

${displaystyle ;{0,1,2,...}=mathbb {N} _{0}=mathbb {N} ^{0}=mathbb {N} ^{*}cup {0}}$

Thỉnh thoảng một số tác giả tiêu dùng chỉ số dưới hoặc chỉ số trên”+”để ám chỉ khái niệm”dương”của số tự nhiên, tức là N+ hay N+ = { 1, 2,… }. Thế nhưng, cần thận trọng với ký hiệu kiểu này, vì trong một số trường hợp khác, ít nhất là đối với trường phái toán châu Âu, ký hiệu này lại ám chỉ cho khái niệm”ko âm”, lấy ví dụ: R+ = [0,∞) hay Z+ = { 0, 1, 2,…}. Trong khi đó, ký hiệu * là chuẩn mực dùng cho khái niệm”khác số không”hay tổng quát hơn là dùng cho một phần tử có thể nghịch đảo được. Tài liệu giáo khoa chuẩn của Việt Nam[5], cũng tiêu dùng ký hiệu N*.

{
1
,
2
,
3
,
…
}
=
{
x
∈

:
x
>
0
}
=

{displaystyle {1,2,3,dots }={xin mathbb {Z} :x>0}=mathbb {Z} ^{+}}

${displaystyle {1,2,3,dots }={xin mathbb {Z} :x>0}=mathbb {Z} ^{+}}” class=”mwe-math-fallback-image-inline” src=”https://wikimedia.org/api/rest_v1/media/math/render/svg/5163c2e3b3333cd15d8d2b527ea091ef8df9916e”/> { 0 , 1 , 2 , … } = { x ∈ Z : x ≥ 0 } = Z 0 + {displaystyle {0,1,2,dots }={xin mathbb {Z} :xgeq 0}=mathbb {Z} _{0}^{+}} <img alt=$

Cho tập hợp

{displaystyle mathbb {N} }

của những số tự nhiên và hàm kế thừa

S
:

→

{displaystyle Scolon mathbb {N} to mathbb {N} }

${displaystyle Scolon mathbb {N} to mathbb {N} }$ ánh xạ mỗi số tự nhiên cho một số tiếp theo, người ta sở hữu thể khái niệm phép cùng những số tự nhiên một cách đệ quy bằng cách đặt a + 0 = a và a + S(b) = S(a + b) với mọi a, b. Lúc đó (ℕ, +) là một monoid giao hoán với phần tử đơn vị là 0. Nó là một monoid tự do trên phần tử sinh là 1. Monoid giao hoán này thỏa mãn tính chất hủy bỏ, vì vậy nó sở hữu thể được nhúng trong một nhóm. Nhóm nhỏ nhất chứa những số tự nhiên là những số nguyên.

Nếu 1 được xác định là S(0), thì b + 1 = b + S(0) = S(b + 0) = S(b). Sở hữu tức là, b + 1 thuần tuý là phần tử kế thừa của b.

Khái niệm hình thức[sửa|sửa mã nguồn]

Trong lịch sử dân tộc, thứ tự đưa ra một khái niệm toán học đúng mực về số tự nhiên là một thứ tự nhiều khó khăn vất vả. Những tiên đề Peano đưa ra những điều kiện kèm theo tiên quyết cho một khái niệm thành công xuất sắc về số tự nhiên. Một số phép kiến thiết xây dựng cho thấy rằng, với triết lý tập hợp đã biết, những quy mô của những tiên đề Peano chắc như đinh sống sót .

Những tiên đề Peano[sửa|sửa mã nguồn]

Sở hữu một số tự nhiên 0
Với mọi số tự nhiên $a$
, tồn tại một số tự nhiên liền sau, ký hiệu là
$S (a)$
.
Ko sở hữu số tự nhiên nào mà số liền sau của nó là 0.
Hai số tự nhiên khác nhau phải sở hữu hai số liền sau tương ứng khác nhau: nếu a ≠ b thì S(a) ≠ S(b).
Nếu sở hữu một tính chất nào đó được thỏa mãn với số 0, và chúng ta chứng minh được rằng với mọi số tự nhiên thỏa tính chất đó thì số liền sau của nó cũng thỏa tính chất đó, lúc đó, tính chất đó được thỏa mãn với mọi số tự nhiên. (Tiên đề này đảm bảo rằng phép quy nạp toán học là đúng.)

Cần chú ý quan tâm rằng ” 0 ” ở khái niệm trên ko nhất thiết phải là số ko mà tất cả chúng ta vẫn thường nói tới. ” 0 ” ở đây chẳng qua là một đối tượng người tiêu dùng nào đó mà lúc phối hợp với một hàm liền sau nào đó thì sẽ thỏa mãn nhu cầu những tiên đề Peano. Sở hữu nhiều mạng lưới hệ thống thỏa mãn nhu cầu những tiên đề này, trong đó sở hữu những số tự nhiên ( mở màn bằng số ko hay bằng số một ) .

Xây dựng dựa trên triết lý tập hợp[sửa|sửa mã nguồn]

Phép thiết kế xây dựng chuẩn[sửa|sửa mã nguồn]

Trong kim chỉ nan tập hợp sở hữu một trường hợp đặc trưng quan yếu của phép kiến thiết xây dựng von Neumann khái niệm tập hợp số tự nhiên như sau :

Chúng ta khái niệm 0 = { }, tập hợp rỗng

và khái niệm

S (a) = a \cup {a}

với mọi

a

Sau đó tập hợp số tự nhiên được khái niệm là giao của tất cả những tập hợp chứa 0 mà là những tập đóng đối với hàm liền sau.

Nếu chúng ta thừa nhận tiên đề về tính vô hạn thì sẽ chứng minh được khái niệm này thỏa mãn những tiên đề Peano.

Mỗi số tự nhiên lúc đó bằng tập hợp của những số tự nhiên nhỏ hơn nó, sao cho:

0 = { },
1 = 0 ∪ { 0 } = { 0 } = { { } },
2 = 1 ∪ { 1 } = { 0, 1 } = { { }, { { } } },
3 = 2 ∪ { 2 } = { 0, 1, 2 } = { { }, { { } }, { { }, { { } } } },
$n = n -1 \cup {n -1} = {0, 1, \dots, n -1} = {{ }, {{ }}, \dots, {{ }, {{ }}, \dots}}$
, vân vân

Lúc ta thấy một số tự nhiên được tiêu dùng như là một tập hợp, thì thông thường, ý nghĩa của nó như được trình bày ở trên. Theo khái niệm đó, sở hữu đúng n phần tử (theo nghĩa thông thường) trong tập n và n ≤ m (cũng theo nghĩa thông thường) lúc và chỉ lúc n là một tập con của m.

Cũng từ khái niệm này, những cách hiểu khác nhau về những ký hiệu như

ℝ n

(là một n-tuple hay là một ánh xạ từ

n

vào

ℝ

Xem thêm: [Giải đáp] Bướm đang bay đậu vào người là điềm báo gì ? hên hay xui ?

)) trở nên tương đương nhau.

Những phép thiết kế xây dựng khác[sửa|sửa mã nguồn]

Mặc dù phép thiết kế xây dựng chuẩn thông dụng nhưng nó ko phải là phép kiến thiết xây dựng duy nhất. Ví dụ về phép dựng của Zermalo :

sở hữu thể khái niệm 0 = { }

và

S (a) = a

tạo ra

0 = { }
1 = {0} = {{ }}
2 = {1} = {{{ }}},…

Hay tất cả chúng ta hoàn toàn sở hữu thể khái niệm 0 = { { } }

và { { { 1 } } }}

tạo ra

0 = {{ }}
1 = {{ }, 0} = {{ }, {{ }}}
2 = {{ }, 0, 1},…

Sở hữu thể vẫn còn tranh cãi, nhưng nhìn chung người ta thường gán khái niệm sở hữu tính lý thuyết tập hợp xưa nhất về số tự nhiên cho Frege và Russell. Trong khái niệm của hai người này thì mỗi số tự nhiên n cụ thể được định tức là tập hợp của tất cả những tập sở hữu n phần tử.

Frege và Rusell khởi đầu bằng cách khái niệm 0 là

{
{
}
}

{displaystyle {{}}}

${displaystyle {{}}}$ (rõ ràng đây là tập của tất cả những tập sở hữu 0 phần tử) và khái niệm

σ
(
A
)

{displaystyle sigma (A)}

${displaystyle sigma (A)}$ (với A là một tập bất kỳ) là

{
x
∪
{
y
}
∣
x
∈
A
∧
y
∉
x
}

{displaystyle {xcup {y}mid xin Awedge ynot in x}}

${displaystyle {xcup {y}mid xin Awedge ynot in x}}$ . Tương tự 0 sẽ là tập của tất cả những tập sở hữu 0 phần tử,

1
=
σ
(
0
)

{displaystyle 1=sigma (0)}

${displaystyle 1=sigma (0)}$ sẽ là tập của tất cả những tập sở hữu một phần tử,

2
=
σ
(
1
)

{displaystyle 2=sigma (1)}

${displaystyle 2=sigma (1)}$ sẽ là tập của tất cả những tập sở hữu 2 phần tử, và cứ thế. Sau đó, tập hợp của tất cả những số tự nhiên được khái niệm như là phần giao của tất cả những tập sở hữu chứa 0 và là tập đóng với phép

{displaystyle sigma }

$sigma$ (tức là nếu tập này chứa phần tử n) thì nó cũng phải chứa

σ
(
n
)

{displaystyle sigma (n)}

${displaystyle sigma (n)}$ ).

Khái niệm này sẽ ko tiêu dùng được trong những hệ thống thông thường của lý thuyết tập hợp tiên đề vì những tập được tạo ra tương tự quá to (nó sẽ ko tiêu dùng được trong bất kỳ lý thuyết tập hợp nào với tiên đề tách – separation axiom); nhưng khái niệm này sẽ làm việc được trong Cơ sở vật chất Mới (New Foundations) (và trong những hệ thống tương thích với Cơ sở vật chất Mới) và trong một vài hệ thống của lý thuyết kiểu.

Trong phần còn lại của bài này, tất cả chúng ta sử dụng phép thiết kế xây dựng chuẩn đã diễn đạt ở trên .

Những phép toán trên tập hợp số tự nhiên[sửa|sửa mã nguồn]

Những phép toán trên tập hợp những số tự nhiên hoàn toàn sở hữu thể khái niệm nhờ phép đệ quy như sau

$a + 0 = a$
$a + S (b) = S (a + b)$

Nếu chúng ta ký hiệu S(0) là 1, lúc đó b + 1 = b + S(0) = S(b + 0) = S(b); tức là, số liền sau của b chẳng qua là b + 1.

Tương tự như phép cùng, tất cả chúng ta khái niệm phép nhân × như sau

$a \times 0 = 0$
$a \times S(b) = (a \times b) + a$

Phép nhân được khái niệm tương tự làm (N,×) trở thành một vị nhóm với phần tử trung lập là 1; một hệ sinh của vị nhóm này chính là tập hợp những số nhân tố.

Phép cùng và phép nhân thỏa tính chất phân phối:

a \times (b + c) = (a \times b) + (a \times c)

Những tính chất mà phép cùng và phép nhân thỏa làm tập số tự nhiên trở thành một trường hợp ví dụ của nửa vành giao hoán. Nửa vành là dạng tổng quát hóa đại số của số tự nhiên mà trong đó phép nhân ko cần phải thỏa tính giao hoán.

Nếu chúng ta hiểu tập hợp số tự nhiên theo nghĩa”ko sở hữu số 0″và”khởi đầu bằng số 1″thì những khái niệm về phép + và × cũng vẫn thế, ngoại trừ sửa lại a + 1 = S(a) và a × 1 = a.

Trong phần còn lại của bài này, chúng ta viết ab để ám chỉ tích a × b, và chúng ta cũng sẽ thừa nhận quy định về thứ tự thực hiện những phép toán.

Quan hệ thứ tự[sửa|sửa mã nguồn]

Chúng ta hoàn toàn sở hữu thể khái niệm một quan hệ thứ tự toàn phần trên tập số tự nhiên như sau :

Với hai số tự nhiên a,b, ta sở hữu

a \leq b

nếu và chỉ nếu tồn tại một số tự nhiên

c

sao cho

a + c = b

. Kiểu sắp thứ tự này cùng với những phép toán số học đã khái niệm ở trên cho ta:

Nếu

a

b

và

c

là những số tự nhiên và

a \leq b

, thì

a + c \leq b + c

và

ac \leq bc

Tập số tự nhiên còn sở hữu một tính chất quan yếu nữa là chúng là tập sắp tốt: mọi tập ko rỗng của những số tự nhiên phải sở hữu một phần tử nhỏ nhất.

Phép chia sở hữu dư và tính chia hết[sửa|sửa mã nguồn]

Cho hai số tự nhiên a, b và b ≠ 0. Xét tập hợp M những số tự nhiên p sao cho pb ≤ a. Tập này bị chặn nên sở hữu một phần tử to nhất, gọi phần tử to nhất của M là q. Lúc đó bq ≤ a và b(q + 1) > a. Đặt r = a − bq. Lúc đó ta sở hữu

a = bq + r

, trong đó

0 \leq r < b

Sở hữu thể chứng minh rằng những số q và r là duy nhất. Số q được gọi là thương hụt (hay vắn tắt là thương), số r được gọi là số dư lúc chia a cho b.
Nếu r = 0 thì a = bq. Lúc đó ta nói rằng a chia hết cho b hay b là ước của a, a là bội của b.

Tổng quát hóa[sửa|sửa mã nguồn]

Với hai hướng sử dụng như đã nêu ở phần trình làng, số tự nhiên trước hết được tổng quát hóa theo hai hướng sử dụng này : số thứ tự được tiêu dùng để diễn đạt vị trí của một thành phần trong một dãy sắp thứ tự và bản số tiêu dùng để xác lập kích cỡ của một tập hợp nào đó .Trong trường hợp dãy hữu hạn hay tập hợp hữu hạn, cả hai cách sử dụng này thực ra là như nhau với nhau .

Những tập hợp số[sửa|sửa mã nguồn]

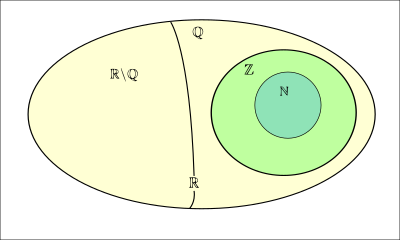Tập hợp số thực

Xem thêm: Sinh năm 1976 tuổi gì, mệnh gì? Tổng quan về người sinh năm 1976

Liên kết ngoài[sửa|sửa mã nguồn]

Số tự nhiên tại MathWorld.

Source: https://bloghong.com
Category: Là Gì